How to share a secret, infinitely
1. Introduction
秘密共享是一种将秘密信息在 $n$ 方之间进行分配的方法,通过这种方法,任何符合条件的子集(授权子集, qualified subset)都可以重构该秘密,而任一不符合条件的子集(非授权子集, unqualified)对该秘密一无所知。授权子集的集合称为访问结构(Access Structure)。
秘密共享方案设计的重要目标就是尽可能最小化份额大小,即各参与方所掌握的关于秘密的信息。
1.1 一些秘密共享方案
- Ito、Saito 和 Nishizeki [ISN93]的研究表明,将份额视为布尔函数时,其大小与访问结构的depth 2 complexity成正比;
- Benaloh 和 Leichter [BL90] 提出了一种方案,其共享大小与访问结构的monotone formula complexity成多项式关系;
- Karchmer 和 Wigderson [KW93]对这一构造进行了概括,使其大小成为monotone span program complexity的多项式。
值得注意的是,这些方案的份额大小的确定都是在确定参与者数量上限(upper bound)的前提下得出的。
1.1.1 Shamir方案[SHA79]的回顾
The dealer holding a secret bit $s$, samples a random polynomial $p(\cdot)$ of degree $k−1$ with coefficients over $GF(q)$, where the free coefficient is fixed to be $s$, and gives party $i\in [n]$ the field element $p(i)$. $q$ is chosen to be the smallest prime (or a power of a prime larger than $n$. (for fairly perfect security)
每一方的份额都是 $GF(q)$ 字段中的一个元素,可以用 $\text{log} q≈ \text{log} n$ 位来表示。
在Shamir的方案中,有限域的阶 $q$ 需要根据参与方数量确定。而大多数情况下,参与方的具体数量可能只有一个范围,但是并不确定,如何在不知道具体参与方数量 $n$ 的情况下确定 $q$ 呢?
[KNY17]就假设参与方的数量是不确定的,并且可能是one-by-one不断增加的。然后给第 $t$ 个参与方尽可能小(大小是关于 $t$ 的函数)的份额。参与方one-by-one的加入,当达到授权子集规定的人数时,就可以重构秘密。
文中所说的 infinite 并不是指参与人数无上限,因为后文中提到参与方 $t\in\mathbb{N}$ ,所以,参与方数量还是有一个上限的,只不过这个上限我们不确定。
参与者不断增加导致的访问结构的改变是单调(monotone)的。也就是说,参与者的加入,不会影响已有的授权集合。
1.2 定义
1.2.1 The standard setting of (perfect) secret sharing
Let $\mathcal{P}_n = {1,\cdots,n}$ be a set of $n$ parties. A collection of subsets $\mathcal{A} \subseteq 2^{\mathcal{P}_n}$ is monotone if for every $B \in \mathcal{A}$, and $B \subseteq C$ it holds that $C \in \mathcal{A}$.
1.2.2 Access Structure
An access structure $A \subseteq 2^{\mathcal{P}_n}$ is a monotone collection of subsets. Subsets in $\mathcal{A}_n$ are called qualified and subsets not in $\mathcal{A}$ are called unqualified.
1.2.3 Threshold access structure
For every $n \in \mathbb{N}$ and $1 \le k \le n$, let $(k, n)$-THR be the threshold access structure over $n$ parties which contains all subsets of size at least $k$.
1.2.4 Evolving access structure
A (possibly infinite) sequence of access structures ${{ \mathcal{A}_ t }}_ {t\in \mathbb{N}}$ is called $\texttt{evolving}$ if the following conditions hold:
1) For every $t \in \mathbb{N}$ , it holds that $\mathcal{A}_ t$ is an access structure over $t$ parties. 2) For every $t \in \mathbb{N}$, it holds that $\mathcal{A}_ t| _ {t-1}$ is equal to $\mathcal{A}_ {t-1}$.
1.2.5 Evolving threshold access structure
For every $k \in \mathbb{N}$, let evolving $k- \texttt{THR}$ be the evolving threshold access structure which contains for any access structure in the sequence all subsets of size at least $k$.
2. Warm-Up
[BR89]提出了一个利用无向图(undirected graph)构建秘密共享方案的思想。简单来说,无向图 $G=(V;E)$ 中每个顶点都对应一个标签,每个参与方的份额对应于两个顶点确定的一条边;存在着两个确定的顶点,记为 $s$ 和 $t$。当且仅当参与方的集合包含从 $s$ 到 $t$ 的路径时,该集合才算是授权集合(qualified set)。
- $s\in {0,1}$ be the secret. Each vertex $v\in V$ assigned a lable.
- For $v = s$ the label is $\omega_s = s$, for $v = t$ the label is $\omega_t = 0$ and for the rest of the vertices the label is chosen independently uniformly at random $\omega_v\leftarrow {0,1}$.
- The share of a party $e=(u,v)\in E$ is $\omega_u\oplus\omega_v$.
- Correctness: \((\omega_ {v_ 1}\oplus\omega_ {v_ 2})\oplus(\omega_ {v_ 2}\oplus\omega_ {v_ 3})\oplus\cdots\oplus(\omega_ {v_ {k- 1}}\oplus\omega_ {v_ k})=\omega_ {v_ 1}\oplus\omega_ {v_ k}=s\)
3. A Scheme for General Evolving Access Structures
3.1 Theorem
对任一evolving access structure,都存在一秘密共享方案,其中第 $t$ 个参与方的共享份额大小为 $2^{t-1}$。
这种构造受 Benaloh 和 Leichter [BL90] 的影响,它给出了任何(标准)访问结构 $\mathcal{A}$ 的秘密共享方案,其特征函数 $1_{\mathcal{A}}$ 由单调公式描述。单调公式(monotone formula)是一棵二叉树,树中的每一片叶子都标有一个输入变量,每一个内部节点都标有一个 $\wedge$ 或 $\vee$ 门。树的根是输出门。
3.2 Construction
\(f(x_ 1,\cdots,x_ n) = (x_ n \wedge f(x_ 1,\cdots, x_ {n-1},1)) \vee f(x_ 1,\cdots,x_ {n-1}, 0)\)
- 公式中的每个门都被分配到一个标签(一个比特);
- 叶子节点的标签对应于参与方的份额;
- 根节点分配到秘密 $s\in{0,1}$;
- 如果一个门已经分配了标签 $v$ ,而它的叶子还没分配标签,则递归应用以下分配规则:
- 如果父节点是 $\vee$ 门, 则给它的两个叶子都分配标签 $v$;
- 如果父节点是 $\wedge$ 门,则随机抽取一个 $u\leftarrow{0,1}$ 并给其中一个孩子分配标签 $u$ ,给另一个孩子分配标签 $v\oplus u$。
- 第 $i$ 个参与方的秘密份额由第 $i$ 个输入变量相对应的所有叶子标签组成。
当 $t=1$ 时,即只有一个参与方时,访问结构 \(f_ 1:\ \ f_ 1(x_ 1) = (x_ 1 \wedge f_ 1(1)) \vee f_ 1(0)\) 当 $f_ 1(1)=1$ 时,Party 1获得标签 $s$,当 $f_ 1(1)=0$ 时,获得标签 $r(1)$。
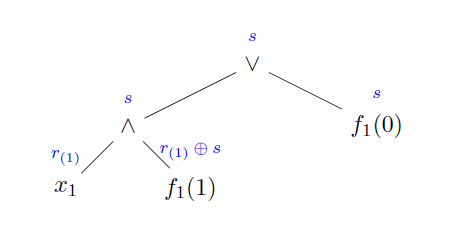
随后,当 $t>1$ 方加入时,访问结构 \(f_{t-1}(b_1,\cdots,b_{t-1})= (x_t \wedge f_t(b_1,\cdots,b_{t-1},1)) \vee f_t(b_1,\cdots,b_{t-1},0)\)
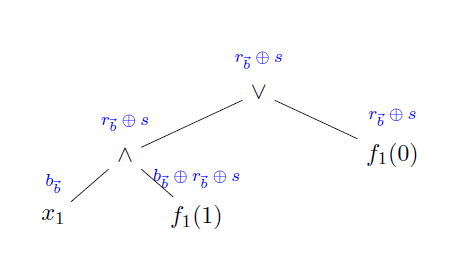
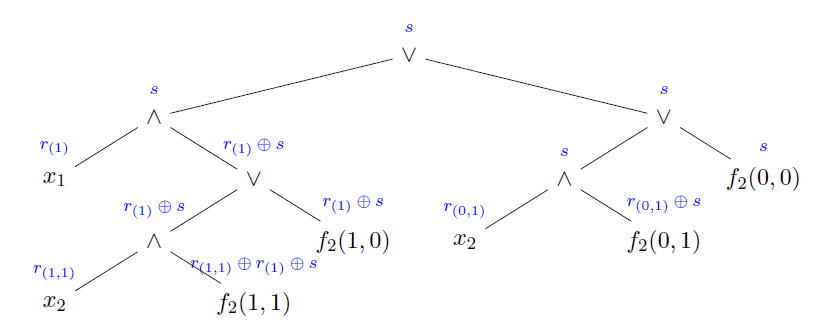
也即是说,当下一个参与方加入时,我们重复采用上述秘密共享方案展开常数项叶子节点。比如,当 $t=2$ 时,得到的二叉树如下图:其中当 $f_2(1, 1) = 1$ 时,Party 2 得到标签 $r(1) \oplus s$ ,反之则得到标签 $r(1,1)$ 。另外,当 $f_2(0, 1) = 1$ 时,Party 2 还会得到标签 $s$ 反之则得到 $r(0,1)$ 。
4. An Efficient Scheme for Evolving 2-Threshold
4.1 Theorem
对任一evolving 2-THR access structure,存在一个秘密共享方案,其中第 $t^{th}$ 参与方的份额大小受到以下约束: \(\text{log}\ t+\text{log}\text{log}\ t+2\text{log}\text{log}\text{log}\ t+6\)
Evolving 2-THR Acess Structure可以通过优化通用结构构造:对 $t \in \mathbb{N}$ 且 $b_1, \cdots, b_t \in {0, 1}$ ,当遇到一个常量叶 $f_t(b_1,\cdots, b_t)$ 的值为 1 时,我们就不需要在以后的步骤中扩展它。事实上,$f_t(b_1,\cdots, b_t)=1$ 意味着 $(b_1, \cdots, b_t)$ 所代表的集合是 qualified。任何包含晚于 t 的各方的子集,包括该子集在内,都可以通过使用 $(b_1, \cdots, b_t)$ 所代表的各方份额来恢复秘密。
4.2 Proof
Lemma:假设存在一种evolving 2-THR access structure的秘密共享方案,其中第 $t$ 方的共享大小为 $\sigma(t)$。那么,存在一种evolving 2-THR access structure的秘密共享方案,其中第 $t$ 方的共享大小为: \(\text{log}\ t+\sigma(\text{log}\ t+1)\)
证明就是反复应用上述引理。

5. A Scheme for Evolving k-Threshold
5.1 Theorem
存在一种evolving k-Threshold access structure的秘密共享方案,其中 $t$ 方的共享份额大小最多为: \((k-1) \cdot \text{log} t + 6k^ 3 \cdot \text{log}\text{log} t \cdot \text{log}\text{log}\text{log} t + 7k^ 4 \cdot \text{log} k\)
5.2 Proof
**Lemma: **假设存在一种evolving k-Threshold access structure的秘密共享方案,其中第 $t$ 方的共享大小为 $\sigma(t)$。那么,存在一种evolving k-Threshold access structure的秘密共享方案,其中第 $t$ 方的共享大小最多为: \((k-1) \text{log} t + k \cdot\sigma(\text{log} t + k) + k^2\)
证明思路同样反复应用上述引理。
Reference
- [BR89] [Josh Cohen Benaloh and Steven Rudich. Unpublished. Private Communication with Steven Rudich, 1989.]