A $(t,n)$ multi-secret sharing scheme
1. Introduction
1979年,Shamir [SHA79]和Blakley [BLA79]提出了 $(t,n)$ 门限方案,其中Shamir的方案是基于拉格朗日插值多项式,而Blakley的方案是基于线性射影几何。
然而,Shamir和Blakley的方案都是单秘密方案,也就是说一次只能分享一个秘密。如果分发者有多个秘密需要分享,就需要多次构造,这无疑是对计算和通信资源的浪费。因此,在此种应用需求下,多秘密共享方案就应运而生了。
1994年,He等人[HE94]提出了基于单向函数和公共移位技术(Public Shift Tech.)共享多个秘密的多级秘密共享(Multistage Secret Sharing MSS)方案,可按预定顺序逐级重构多个秘密。
1995年,He等人[HE95]提出了一个基于双变量单向函数的动态多秘密共享方案。其中,双变量单向函数可以有效避免秘密份额的暴露问题,而“动态”则体现在秘密持有者能够公布他/她想要共享的秘密的一些信息。
2000年,Chien等人[CHIEN00]提出了一个基于系统分组码的多重秘密方案。该方案具有以下特点,(1)它允许并行秘密重构;(2)秘密持有者可以动态确定共享秘密的数量;(3)构造生成矩阵简单有效;(4)是多用途方案;(5)计算效率高。
Chien等人方案中秘密可以被同时重构的思想能有效降低计算和通信开销,因此,Yang等人[YANG04]在此基础上,提出了基于Shamir门限方案的多秘密共享方案。该方案使用了双变量单向函数,满足Chien等人方案的优点,并且效率更高。
2. 双变量单向函数
函数 $f(r,s)$ 表示将秘密 $s$ 和随机值 $r$ 映射到固定长度的字符串上的双变量单向函数。它具有以下性质: 1) 给定 $r$ 和 $s$ ,很容易计算出 $f(r,s)$ ; 2) 给定 $f(r,s)$ 和 $s$ ,很难计算出 $r$ 。 3) 在不知道 $s$ 的情况下,给定任一 $r$ ,很难计算出 $f(r,s)$ 。 4) 给定 $s$ ,很难找到两个不等的 $r_ 1$ 和 $r_2$ ,使得 $f(r_ 1,s)=f(r_ 2,s)$ 。 5) 给定 $f(r,s)$ 和 $r$ ,很难计算出 $s$ 。 6) 给定 $f(r,s)$ 和 $r$ ,很难计算出 $f(r’,s)$ ,其中 $r’\neq r$ 。
3. Yang等人方案描述
3.1 符号说明
| 符号 | 描述 |
|---|---|
| $s_ i$ | 第 $i$ 个秘密 |
| $f(r, s)$ | 双变量单向函数 |
| $p$ | 要共享的秘密数 |
| $P_ i$ | 第 $i$ 个要共享的秘密( $i\le p$ ) |
3.2 初始化
秘密拥有者首先随机选择 $n$ 个秘密份额 $s_ 1,s_ 2,\cdots,s_ n$ 并通过秘密信道将他们分发给参与者。(这里体现了动态性)
3.3 分发阶段
分发阶段需要分为两种情况讨论,第一种是 $p\le t$,也即需要共享的秘密数少于门限值;另一种情况是 $p>t$ ,即需要共享的秘密数大于门限值。
$p\le t$
随机选择素数 $q$ 并构造 $t-1$ 次多项式 $h(x)$ mod $q$ ,如下:
\[h(x)=P_ 1+P_ 2x^ 1+\cdots +P_ px^ {p-1}+a_ 1x^ p+a_ 2x^ {p+1}+\cdots +a_ {t-p}x^ {t-1} \text{ mod } q\]其中, $0< P_ 1,P_ 2,\cdots,P_p,a_ 1,a_ 2,\cdots,a_ {t-p}<q$ 。
然后计算 $y_ i=h(f(r,s_ i)) \text{ mod } q$,其中 $i=1,2,\cdots, n$ 。
最后公布 $(r,y_ 1,y_2,\cdots,y_ n)$ 。(注意,这里的公布方式需要在认证的前提下进行。)
$p> t$
随机选择素数 $q$ 并构造 $p-1$ 次多项式 $h(x)$ mod $q$ ,如下:
\[h(x)=P_ 1+P_ 2x^ 1+\cdots +P_ px^ {p-1} \text{ mod } q\]其中, $0< P_ 1,P_ 2,\cdots,P_p<q$ 。
然后计算 $y_ i=h(f(r,s_ i)) \text{ mod } q$ ,其中 $i=1,2,\cdots, n$ 。
再对 $i=1,2,\cdots, p-t$ 计算 $h(i) \text{ mod } q$ 。
最后公布 $(r,h(1),h(2),\cdots,h(p-t),y_ 1,y_ 2,\cdots, y_ n)$ (同样通过认证的方式)。
3.4 重构阶段
同样,重构阶段也分为两种情况
$p\le t$
至少 $t$ 个参与者汇集他们的份额 $f(r,s_ i),\text{ for }i=1,2,\cdots,t$ ,利用拉格朗日插值重构,计算如下:
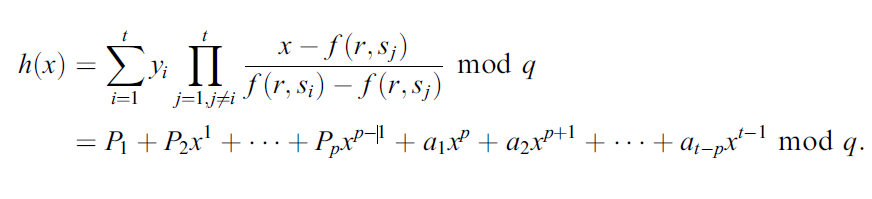
$p> t$
除了需要至少 $t$ 个参与者汇集他们的份额 $f(r,s_ i)\text{ for }i=1,2,\cdots,t$ 之外,还需要分发者公布的 $h(i),\text{ for }i=1,2,\cdots,p-t$ 。当拥有 $t$ 对 $(f(r,s_ i),y_ i)$ 和 $p-t$ 对 $(i,h(i))$ 值时,可以通过拉格朗日插值确定唯一 $p-1$ 次多项式 $h(x)$ ,计算如下:
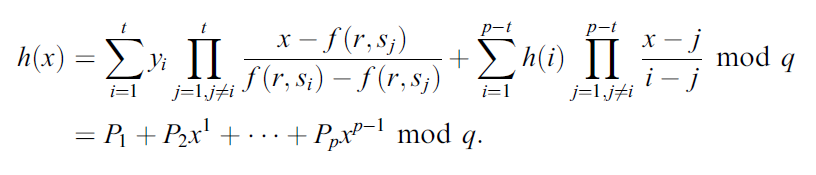
4. 结论
在信息论中,该方案是香农完美安全的。
该方案使用双变量单向函数,使得秘密持有者无须为下一次秘密共享会话重新分发新的秘密份额,只需要改变随机数 $r$ 即可。