RAMP Scheme

Introduction of RAMP Scheme

本文基于门限秘密共享方案，提出了在牺牲部分安全性的前提下更加高效的 $(d,k,n)$ RAMP协议，即将秘密分成 $n$ 份，至少 $k$ 人可以恢复出秘密，少于 $d$ 人无法获得关于秘密的任何信息。其中，$d$ 称为lower threshold，$k$ 称为upper threshold[Douglas18]。

Definition. From these $d$ inputs (and using $k - d$ other predetermined types of inputs, perhaps some of them random) it produces $n$ outputs in such a fashion that the $d$ inputs can easily be reconstructed from any $k$ outputs. But there is a predetermined level of uncertainty (perhaps the level is zero, and there is an absolute upper bound dependent on $j$) regarding the inputs if only $j$ outputs are known – given that $j < k$. It should be obvious from the description above that the assumption $1\le d\le k\le n$ is implicit in this definition.

在另一篇文章里[Santis99]，是这样描述的：

Definition. A $(t, k, n, S)$ ramp scheme is a protocol to distribute a secret $s$ chosen in $S$ among a set $P$ of $n$ participants in such a way that: 1) sets of participants of cardinality greater than or equal to $k$ can reconstruct the secret $s$, 2) sets of participants of cardinality less than or equal to $t$ have no information on $s$, whereas 3) sets of participants of cardinality greater than $t$ and less than $k$ might have “some” information on $s$.

从定义中可以看出，基本的线性 $(k,n)$门限方案考虑的是 all-or-none 安全性，即香农完美安全。也即是说，for every word $w$ belonging to the field $\mathbb{F}$ we have: tu1

之所以称之为RAMP方案，是因为关于秘密的不确定性随着获得的关于秘密的知识的增加而减少，见下图。 tu2

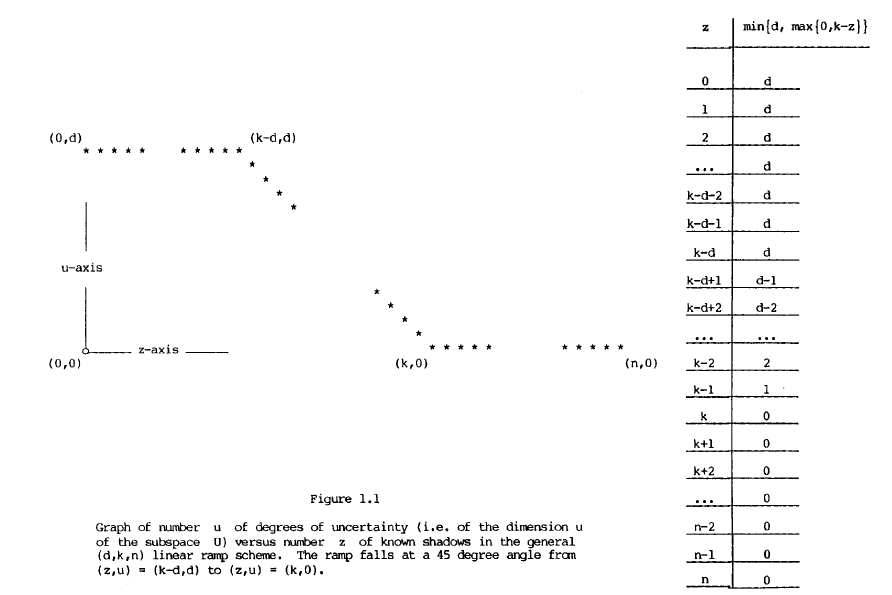
可以说，Shamir门限方案[SH79]是RAMP方案的极端情况，即 $(1,k,n)$ RAMP方案，低于 $k$ 人的情况下，不会获得关于 $s$ 的任何知识。 tu3

而 $k$ out of $n$ p/s/r process[AS81]则是另一种情况，即 $(k,k,n)$ RAMP方案。见下图。 tu4

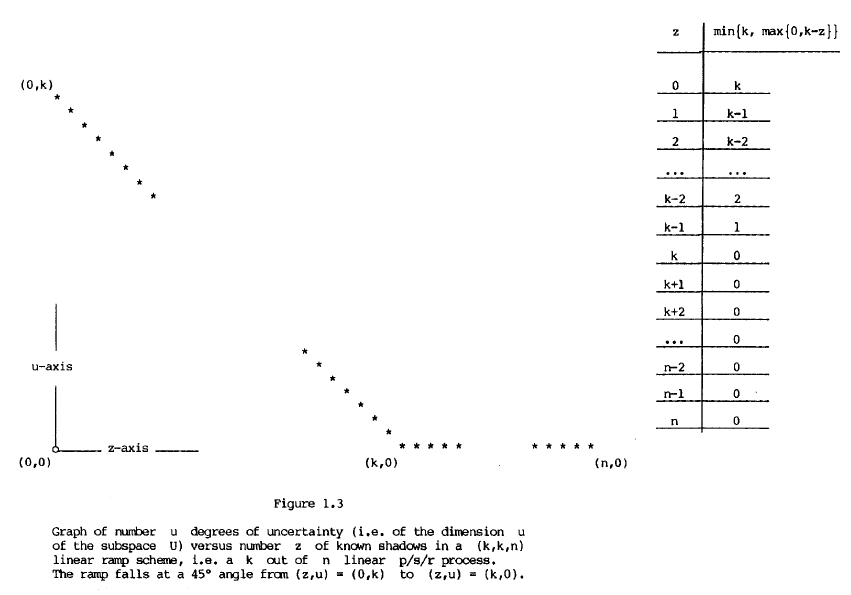
Two examples of applications of ramp schemes are constructing efficient broadcast encryption schemes [broadcast] and ‘‘repairing’’ shares in threshold schemes [repairing]. It is also worth noting that Rabin’s information dispersal algorithm [Labin], which is used for distributed storage, is a special case of ramp schemes.

Shannon perfect security & relative security

香农完美安全的定义如下。考虑由 $f(1),f(2),\cdots,f(d)$组成的 $d$ 维向量空间 $\mathbf{T}$，给定 $z$ shadows的知识，存在 $\mathbf{T}$ 的仿射子空间(affine subspace) $\mathbf{U}$，其维度(dimensionality)为 $dim(\mathbf{U}) = \text{min} { d,\text{max} { 0,k-z } }$，并且具有以下性质：对于每一个 $\xi=(\xi(1),\xi(2),\cdots,\xi(d))$，可以得到：

\[\text{Pro}(\xi\notin\mathbf{U}=0)\] \[\text{Pro}(\xi = w\in\mathbf{U} | z)=\frac{\text{Pro}(\xi = w\in\mathbf{U})}{\text{Pro}(\xi\in\mathbf{U})}\]

tu5

简而言之，拥有来自 $(d,k,n)$ 线性RAMP方案的 $z$ 个shadows的贝叶斯对手现在知道期望的列表 $\xi\in\mathbf{U}$。这比他在开始知道任何阴影之前所拥有的信息量有了相当大的增加。但是所获得的这些知识又不足以让他轻而易举的恢复出秘密。

Shamir (d,k,n)-ramp方案

初始化

设素数 $p≥v+1$，定义 $t_0=k-d$，设 $\mathcal{K}=(\mathbb{Z}_p)^{t_0}$ , 定义值 $x_1,x_2,\cdots,x_v$ 为 $\mathbb{Z}_p$ 中的 $v$ 个不同的非零元，对于所有的 $1\le i\le v$，$D$ 将 $x_i$ 给 $P_i$，其中 $x_i$ 是公开的信息。

共享分发

设 $D$ 想要共享秘密 $K=(a_0, \cdots, a_{t_0-1})$ 。首先，$D$ 从 $\mathbb{Z}_ p$ 中独立而随机地选择 $a_ {t_0}, \cdots, a_ {k-1}$ 。从而 $D$ 定义: $a(x)=\sum_ {j=0}^{k-1}a_ j x^j$ 。这里的 $a(x)$ 是一个随即多项式（独立随机选择 $a_ {t_ 0},\cdots,a_ {k-1}$ 保证了其随机性），其中次数最大为 $k-1$ 。这样，前 $t_ 0$ 个前个系数包含了秘密 $K$ 。

对 $1\le i\le v$，$D$ 构造共享 $y_ i=a(x_ i)$，并共享 $y_ i$ 给 $P_i $。

RIGID LINEAR SCHEMES

这里需要用到超平面的概念：超平面是 $n$ 维欧氏空间中余维度等于一的线性子空间，也就是必须是 $(n-1)$ 维度。可以想象成线中的一点，或者面中的一条线，或者空间中的一个面。 $n$ 维空间 $F^n$ 中的超平面是由方程：$a_ 1x_ 1+\cdots+a_ nx_ n=b$ 定义的子集，其中 $a_ 1, \cdots, a_ n \in F$ 是不全为零的常数。或者也可以表示成向量的形式： $\begin{pmatrix} a_ 1 & a_ 2 & \cdots & a_ n \end{pmatrix}\begin{pmatrix} x_ 1 \\ x_ 2 \\ \cdots \\ x_ n \end{pmatrix}=b$

举例：秘密为三维空间的一点 $(x,y,z)$

分发者 $D$ 计算如下： $\begin{cases} ax+by+cz=c(1) \\ ax+by+cz=c(2) \\ ax+by+cz=c(3) \end{cases}$ 其中 $c(\cdot)$ 代表常数，$D$ 将三个方程分别分发给 $P_ 1, P_ 2, P_ 3$，即分发的份额是“超平面”（这里就是一个平面）， $d$ 个超平面可以获得一些信息，比如这里，两个平面能够确定秘密点 $(x,y,z)$ 所在的直线，然而并不能恢复秘密。

文章中还介绍了根据其他方案构造的ramp方案，内容较多，这里不一一列举了。